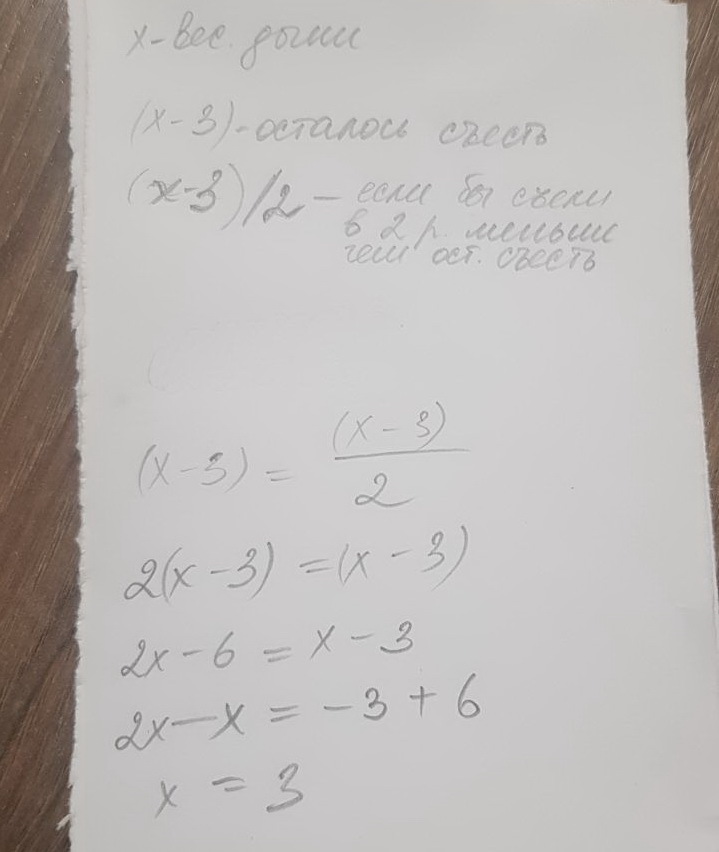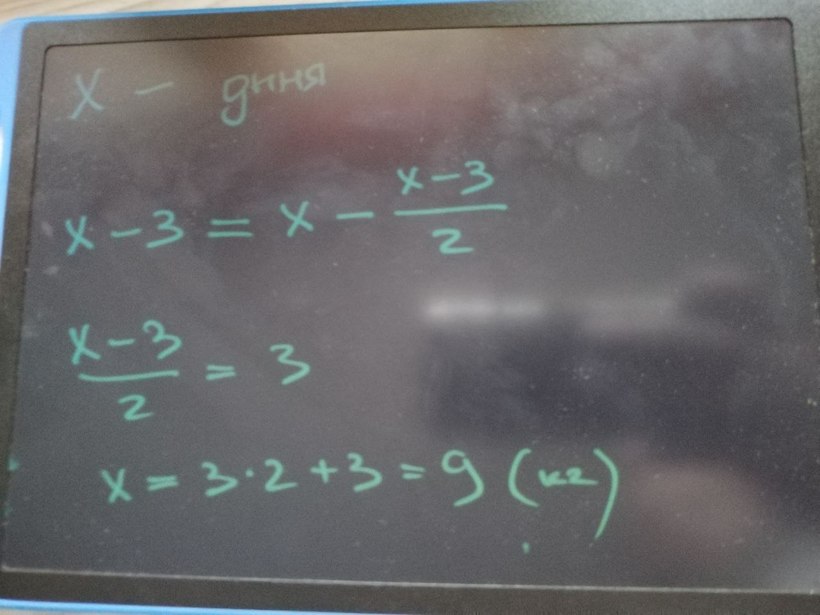Дыня беспредела: 4-классникам предложили решить простую задачу. Наши читатели помогли

Уведите от экрана детей. У нас сегодня задача про дыню. Наконец-то реальная ситуация из жизни, а не эти ваши абстрактные дискриминанты. Читатель, приславший задачу, утверждает, что такая есть в некоем пособии для четвертого класса, но мы сомневаемся. Как бы то ни было, попробуйте найти ответ (пользуясь инструментами и формулами для четвертого класса). Но будьте осторожны, эти дыни довольно коварны.

Важно понимать — это задача не из обычной школьной программы для четвертого класса, она предназначена для дополнительных занятий и развития логики у олимпиадников. Продублируем условие текстом.

«Съели три килограмма дыни, и осталось съесть столько, сколько осталось бы съесть, если бы съели в два раза меньше, чем столько, сколько осталось съесть. Сколько весила дыня?»

Поговаривают, вместо капсулы с синильной кислотой эта задача находилась в ящике с котом Шредингера. Но мы все же надеемся получить от читателей ответ и варианты решения. Возможно, оно на поверхности и проще, чем кажется. Поделитесь с коллегами, детьми, недругами, займите чем-то ваш трудовой коллектив. Но избегайте рукоприкладства при решении.

Дополнено: варианты решений и ответы

Делить дыню самоотверженно бросились инженеры, пенсионеры, школьники, репетиторы, программисты, гуманитарии и представители прочих сословий. Встали цеха, офисы, СТО, ларьки с шаурмой... Многих задела за живое именно формулировка. Ну и, конечно, нельзя сбрасывать со счетов актуальность научной проблемы.

Методы решения применялись разные (не все для четвертого класса), ответы в итоге тоже различаются. У некоторых в процессе решения дыня преобразовалась в тыкву, что в корне поменяло подходы. Задачу решали на бумажках, мониторах, школьной доске, кто-то прислал вводящее в транс видео. Кто-то срочно телеграфировал: «Я люблю арбуз».

Мы приведем основные доктрины наших читателей. А потом предложим проголосовать за правильный вариант ответа.

Многие сразу принялись строить систему уравнений с двумя переменными. Правда, это чит: системы проходят только в 7-м классе. И все же посмотрим, что получилось.

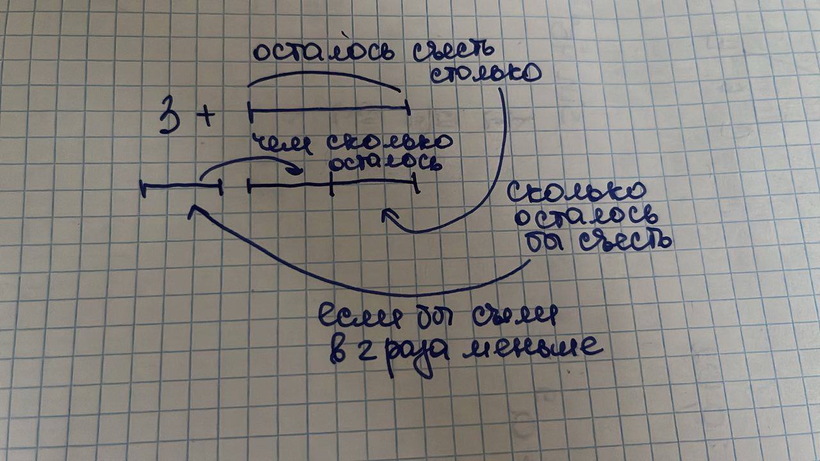
Вес дыни примем как D. Недоеденное — X. Таким образом:

D = 3 кг + X.

При этом из условия (если пробраться сквозь словесные дебри), следует: не доели разность между весом дыни D и половинкой икса.

X = D – X/2.

Из этой пары простейших уравнений в несколько действий находим: X = 6 кг.

Осталось найти вес исходной дыни: D = 3 + 6 = 9.

Получается, дыня весила 9 кг.

Правда, системы уравнений — тоже не бесспорная штука. У разных читателей дают разный результат. У кого-то получилось 5, у кого-то 3, у кого-то дыню съели полностью, сколько бы в ней ни было веса...

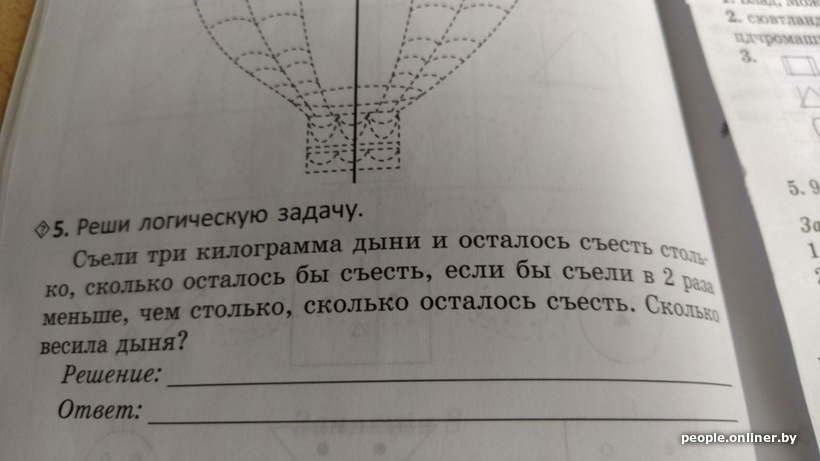
Вот, например, как читательница Анастасия (не только она) получила ответ 6 кг. «X — начальный вес, Y — остаток дыни. Тогда: X – 3 = Y.

Если я правильно понимаю русский, то остается столько же, но изначальный вес надо разделить на 2: Y = X/2.

Система уравнений получится такая:

X – 3 = Y.

X/2 = Y.

Отсюда:

X = 2Y.

2Y – 3 = Y.

Соответственно, Y = 3, X = 6. 

Подставляем в условие: было 6 кг, съели 3 кг, осталось 3 кг. Остаток 3 кг — это столько, сколько осталось бы, если бы съели в два раза меньше».

У Анастасии, кстати, немало сторонников. Мы бы не связывались!

Вот вариант в защиту 6 кг от Елены.

Но системы — это слишком просто. Наша квантовая (или струнная?) дыня умеет весить по-разному в разных системах. (Не исключаем, что без наблюдателя она и не такое вытворяет.) Вот что пишет 52-летний программист по имени Vr+. Он как раз понимает, что при решении надо обойтись без системы уравнений. «Можно привести ряд выкладок с уравнениями, но отталкиваемся от того, что это логическая задача для 4-го класса. Здесь, скорее всего, проходят тему на умножение и деление нуля. Поэтому правильный ответ — 3 кг. Все действия над остатком, то есть нулем, приводят к нулю».

Возможно, мы не до конца поняли тут логику, но в двоичной системе и не такое случается.

Немного экзотических версий (которые не факт, что неправильные).

Читатель Сергей выдвигает смелую гипотезу: дыня весила меньше, чем от нее отъели. Мы не совсем поняли обоснование, но возражать опасаемся: «Думаю, она весит 750 г. Так как, если было 3 кг, от нее отъели в два раза меньше — это 1,5 кг. И осталось в 2 раза меньше. Следовательно — 750 г».

Пользователь Na Shs уверен, что от тыквы ничего не отъедали:

«3 + X = Y

X = X/2

Следовательно, X = 0, а тыква весит 3 кг».

Иван обосновывает, как у него получилось 4,5 кг: «Съели 3 кг (2/3), осталось съесть 1/3. Сколько осталось бы съесть, если бы съели в два раза меньше (1/3), чем столько, сколько осталось съесть (2/3)».

У Павла своя версия событий: «Оставшаяся часть — это половина съеденного, поделенная на 2, получается 0,75. Дыня весит 3,75 кг».

У читателя по имени Raduyk 4,5 кило. Все документы имеются! И инфографика! Он тоже не одинок.

В теории — подходящий для четвероклассника способ предложила репетитор из Гродно Анна Павловна: дыню надо представить в виде отрезка. Не частицы! Получилось 9 кило.

Вариант с дробями тоже хорош — но не уверены, что детвора уже знает дроби.

А теперь — реформа математики! Будем определять правильный ответ голосованием. Никто еще так не делал.

Наш канал в Telegram. Присоединяйтесь!

Есть о чем рассказать? Пишите в наш телеграм-бот. Это анонимно и быстро